Cluster Expansion Model for QCD Baryon Number Fluctuations: No Phase Transition at $\mu_B / T < \pi$

Abstract

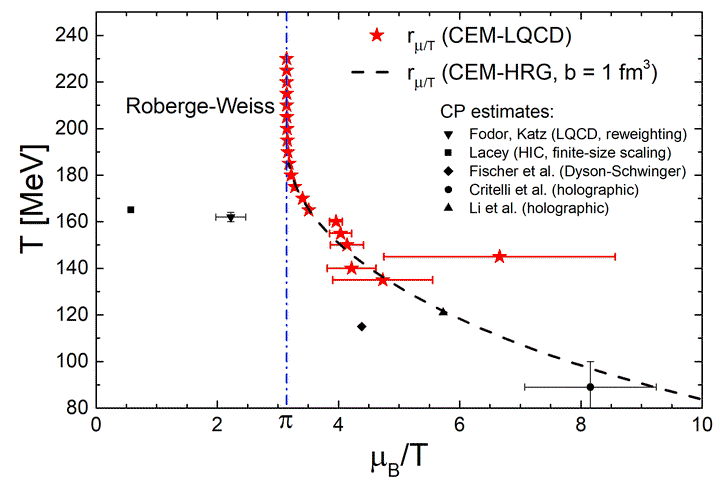
Cluster Expansion Model (CEM), representing a relativistic extension of Mayer’s cluster expansion, is constructed to study baryon number fluctuations in QCD. The temperature dependent first two coefficients, corresponding to the partial pressures in the baryon number $B = 1$ and $B = 2$ sectors, are the only model input, which we fix by recent lattice data at imaginary baryochemical potential. All other coefficients are constructed in terms of the first two and required to match the Stefan-Boltzmann limit at $T \to \infty$. The CEM allows calculations of the baryon number susceptibilities $\chi_k^B$ to arbitrary order. We obtain excellent agreement with available lattice data for the baryon fluctuation measures $\chi_2^B$, $\chi_4^B$, $\chi_6^B$ and predict higher order susceptibilities, that are not yet available from Lattice QCD. The calculated susceptibilities are then used to extract the radius of convergence of the Taylor expansion of the pressure. The commonly used ratio test fails due to the non-trivial asymptotic behavior of the Taylor coefficients. At the same time, a more elaborate estimator provides finite convergence radii at all temperatures and in agreement with the singularities of Pad'e approximants. The associated singularities lie in the complex $\mu_B/T$-plane and appear smoothly connected to the Roberge-Weiss transition at high temperatures and imaginary chemical potential. No evidence for a phase transition at $\mu_B / T \lesssim \pi$ is found.